From Small Investments to Big Dreams: The Role of Compounding in Wealth Creation


Envision generating ₹1 crore out of just ₹10,000 without any significant risks or lottery wins. It sounds like a dream, don't you think? The true strength of compounding, however, is in its ability to increase your wealth over time with little effort. The finest aspect? It's not just for wealthy people or financial professionals. Anyone can use compounding to increase their wealth if they are persistent, patient, and make wise judgements.
We'll go into great detail in this blog post on how to grow that modest ₹10,000 investment into a whopping ₹1 crore. Are you curious about the process? Continue reading for the outcomes that are well worth the wait—the magic is in the maths!
The key to this strategy is the power of compound interest. Compound interest is the interest you earn on both your initial principal and the accumulated interest from previous periods. In the stock market, compounding comes into play when your investments grow year after year, and the returns from one year become the principal for the next year.
The formula to calculate compound interest is:
$$ A = P \times \left( 1 + \frac{i}{100}
\right)^n $$
where:
• 𝐴 = total amount after n years
• 𝑃 = the principal amount (initial investment)
• 𝑖 = annual interest rate (or return on investment)
• 𝑛 = the number of years
Historically, the stock market (e.g., Nifty 50 or Sensex) has provided an average return of 15-20% per year over the long term. Let’s assume

We want to find 𝑛 such that A=1,00,00,000 (₹1 crore).
Using the compound interest formula, we rearrange it to solve for 𝑛:
$$ 1,00,00,000 = 10,000 \times \left( 1 + \frac{15}{100}
\right)^n $$
This simplifies to:
$$ 1000 = ( 1.15)^n $$
$$ log(1000) = log( 1.15)^n $$
$$ log(1000) = nlog( 1.15) $$
$$ n = \frac{\log(1000)}{\log(1.15)} \approx \frac{3}{0.0607} \approx 49.42 \text{ years} $$
With a 15% annual return, it would take approximately 49 to 50 years for ₹10,000 to grow to ₹1 crore.
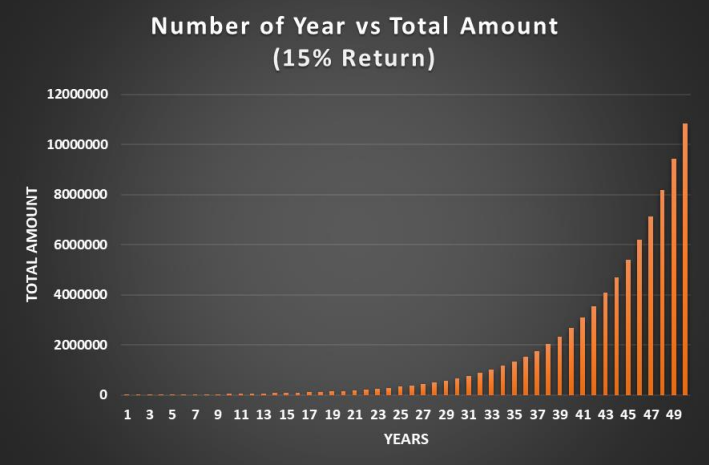
If you invest in individual stocks or mutual funds with a higher average return, say 20% annually, your money grows faster.
Using the same approach:
$$ 1,00,00,000 = 10,000 \times \left( 1 + \frac{20}{100}
\right)^n $$
simplifying to:
$$ 1000 = ( 1.2)^n $$
$$ log(1000) = log( 1.2)^n $$
$$ log(1000) = nlog( 1.2) $$
$$ n = \frac{\log(1000)}{\log(1.2)} \approx \frac{3}{0.0791} \approx 37.92 \text{ years} $$
With a 20% annual return, ₹10,000 grows to ₹1 crore in approximately 38 years.

Example1: Infosys
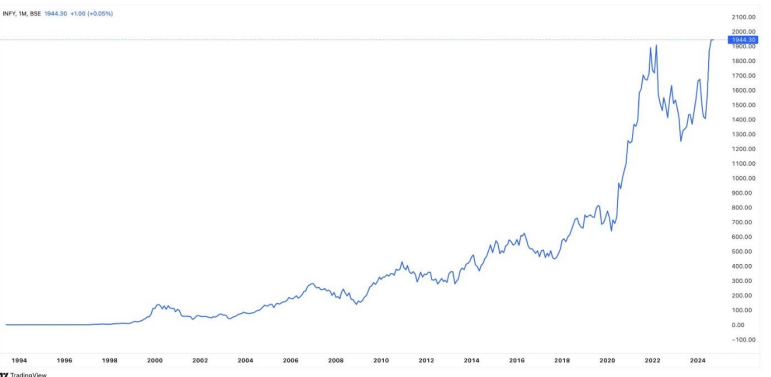
If someone had invested ₹10,000 in Infosys during its IPO in 1993, that investment would be worth over ₹2 crore today, thanks to consistent growth, dividends, and stock splits. Infosys has provided compounded annual growth rates (CAGR) of over 30% in its early years, making it a powerful example of compounding in action.
Example2: HDFC Bank

Similarly, an investment of ₹10,000 in HDFC Bank’s IPO in 1995 would have grown into over ₹1.5 crore by 2021. This is due to the consistent growth in the stock price, along with dividends and compounding over time.
Stock market investing is a long-term endeavour. It is possible to make ₹1 crore with ₹10,000, but it will take time, perseverance, and a dedication to continuing investments. Your investments will continue to increase tremendously in value if you reinvest dividends and let your profits compound.

1. Get Started Early: Your money has more time to grow through compound
interest if
you invest as soon as possible
2. Be Consistent: Regular investments, even in small amounts, can accumulate
significantly over time.
3. Stay Invested: Avoid trying to time the market. Holding for an extended
period of time
makes compounding work to your advantage
4. Concentrate on Growth: : Invest in mutual funds or high-growth stocks that
have a solid
track record.
It takes more than just good fortune to turn ₹10,000 into ₹1 crore; you also need to understand and use compounding. You may accomplish exceptional financial progress and make your money work for you with patient, disciplined investing over the long term.
Now that we've explored how a one-time investment of ₹10,000 can grow into an astounding ₹1 crore over time. But what if we took it a step further and talked about something even more practical — something most of us already do: monthly investments. Wouldn't it be even more exciting to see how regular contributions can grow your wealth even faster with the power of compounding? Intrigued? Let’s explore a real-life scenario where continuous monthly investments make compounding even more fascinating and, trust me, much more convincing! Ready to dive in? Just click the link to keep reading!